生成模型中的素数分布:AI视角的几何学习
生成模型中的素数分布:AI视角的几何学习
1. 训练目标与数据构造
我们将素数间隔序列构造为高维向量:
vn=(pn+1?pn, pn+2?pn+1,…,pn+k?pn+k?1)∈Rkv_n = (p_{n+1}-p_n,\ p_{n+2}-p_{n+1},\dots,p_{n+k}-p_{n+k-1}) \in \mathbb{R}^k
这些向量形成点云,具有高度非线性但低维嵌入特性。
多尺度几何结构: 小尺度下,孪生素数、三生素数形成局部簇;大尺度下,素数定理的渐近规律占主导。生成模型必须具备多尺度捕捉能力,可通过小波变换提取特征并作为条件输入。
2. 模型设计与几何约束
主成分对齐损失
LPCA=∑i=1d(1?cos?∠(u^i, ui))\mathcal{L}_{\mathrm{PCA}}=\sum_{i=1}^d \Big(1-\cos\angle(\hat u_i,\ u_i)\Big)
保证生成数据与真实数据的主子空间一致。
拓扑保持项
LTopo=dbottleneck(D(V^),D(V))\mathcal{L}_{\mathrm{Topo}}=d_{\mathrm{bottleneck}}(D(\hat V),D(V))
保持持久同调的全局形状。
对称性与不变性
间隔分布在缩放、旋转、局部置换下近似不变。设计等变网络嵌入这些先验,提高泛化能力。
算术簇条件化
欧拉多项式与算术级数生成的素数形成特定簇,可作为条件标签指导模型学习。
综合损失:
L=Lgen+λPCALPCA+λTopoLTopo+λsymLsym+λcondLcond\mathcal{L}=\mathcal{L}_{\mathrm{gen}}+\lambda_{\mathrm{PCA}}\mathcal{L}_{\mathrm{PCA}}+\lambda_{\mathrm{Topo}}\mathcal{L}_{\mathrm{Topo}}+\lambda_{\mathrm{sym}}\mathcal{L}_{\mathrm{sym}}+\lambda_{\mathrm{cond}}\mathcal{L}_{\mathrm{cond}}
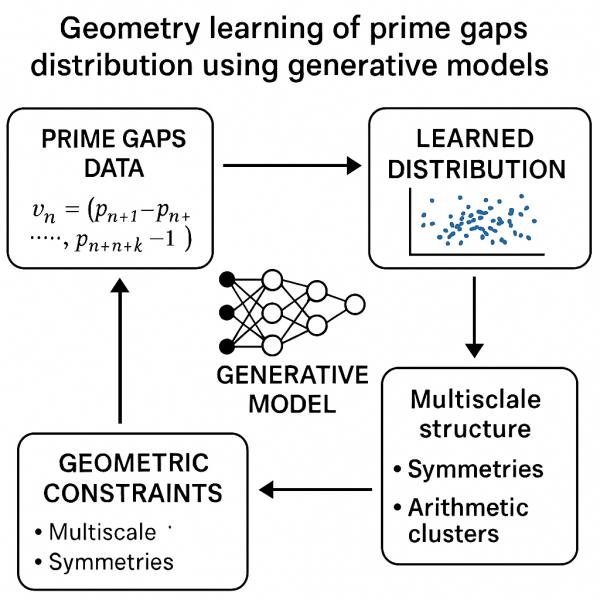
图注: AI生成模型学习素数间隔分布的几何结构流程图。图中展示了从原始素数间隔数据构造(左上),通过神经网络模型进行生成(中间),得到学习后的分布(右上),并通过几何约束(下方)如多尺度结构、对称性与算术簇反馈优化模型。整个过程形成一个闭环,体现了数据驱动与结构约束协同作用于素数几何学习的机制。
3. 已有实验结果
Kolpakov & Rocke (2024, PLOS ONE)
使用最大熵与机器学习方法,AI 能重现 Hardy–Ramanujan 定律的近似。
结果:AI 能学习素数间隔的统计分布,但难以自主发现新定律。
GPAI 团队 (2025)
神经网络能识别孪生素数簇等局部结构。
在大尺度下,模型学到的平均间隔趋势与素数定理一致。
潜空间解释性有限,尚未建立与黎曼零点的直接对应。
生成模型实验(GAN/扩散)
能在高维间隔空间中重建低维嵌入结构。
结果主要是拟合已知规律,而非发现新规律。
局限性总结:
模型只能学习训练数据中的模式,无法外推到极大间隔。
潜空间解释性不足。
规律发现有限,主要是验证已有数论现象。
4. 改进方法与未来方向
多尺度条件化:显式引入小波特征,使模型同时学习局部簇与全局趋势。
等变网络结构:融入旋转、缩放不变性,提高模型对几何对称性的捕捉能力。
算术簇标签:将二次多项式簇、算术级数簇作为条件信息,提升模型对特定模式的学习。
潜空间解释性:使用 β-VAE 或 InfoGAN,促进潜因子解缠,建立潜空间轴与算术性质的对应。
跨领域比较:将素数间隔生成模型与随机矩阵理论、混沌系统的生成模型对比,寻找更深层联系。
开源与基准化:建立公开基准集,比较不同模型的几何—拓扑表现,促进可重复性。
5.结语(增强版)
已有实验表明,AI生成模型确实能够学习素数分布的统计规律与几何特征,重现如素数定理、孪生素数簇、间隔分布的正态近似等经典现象,并在高维间隔空间中构建出与真实数据相似的低维嵌入结构。这些成果验证了素数分布的“可学习性”,也证明了几何视角在数论中的解释力。然而,迄今为止,AI尚未发现新的定理或提出可验证的数论猜想,其潜空间结构与深层算术对象(如黎曼ζ函数零点、模空间上的轨迹)之间的联系仍属未知。
要使AI从“验证工具”跃升为“猜想生成者”,我们提出以下具体改进设想:
1. 多尺度几何分析的深度融合
将小波变换、尺度空间理论与生成模型结构结合,使模型在不同尺度上分别学习局部簇(如孪生素数)与全局趋势(如素数定理)。在训练中引入多尺度损失项,分别对不同频带的几何结构进行约束,并在潜空间中建立尺度因子与几何簇之间的映射。
2. 对称性与不变性嵌入的结构化实现
设计具备旋转、缩放、置换等群等变性的生成网络(如E(2)-等变卷积、置换等变Transformer),使模型在几何变换下保持结构稳定性。通过对称性约束损失项,强化模型对素数分布中隐含对称结构的识别能力,提升泛化性与解释性。
3. 算术簇的条件生成与分层建模
将已知生成素数的算术机制(如欧拉多项式、狄利克雷同余类)作为标签嵌入模型,使其在不同簇上分别学习几何风格。进一步构建“簇内几何保持 + 簇间几何分离”的对比损失,使模型在生成时能区分不同算术来源的结构,并在潜空间中形成可解释的簇分布。
4. 潜空间的语义解缠与因子映射
使用 β-VAE、InfoGAN 等结构促进潜因子的解缠,使每个潜变量对应一个几何或算术特征(如平均间隔、周期性、簇标签)。通过线性探针与非线性回归,将潜空间轴与素数簇、模空间轨迹、ζ函数零点频率等数学对象建立映射关系,探索“潜空间—数论结构”的桥梁。
5. 跨领域结构对比与谱几何分析
将生成模型中学到的几何结构与其他数学领域(如随机矩阵理论、量子混沌、动力系统)中的谱结构进行对比,寻找素数分布与酉群特征值、能级间隔、重正化群不动点之间的几何对应。通过谱统计与拓扑不变量的比较,构建跨领域的结构类比与猜想生成机制。
6. 开源实验平台与可验证猜想生成
建立开放的素数几何生成平台,提供标准数据集、模型结构、评估指标与可视化工具,鼓励研究者在不同簇、不同尺度、不同模型下生成数据并提出猜想。通过自动化的几何—算术分析模块,将生成数据中的规律转化为可验证的数论猜想,并与已有理论进行对比与归纳。
综上所述,AI生成模型在素数分布研究中的角色正在从“拟合者”向“结构发现者”转变。通过引入多尺度分析、对称性嵌入、算术簇条件化、潜空间解释性与跨领域结构对比,我们不仅可以提升模型的几何保形能力,更可能在潜空间中发现隐藏的数论结构,从而提出新的猜想。这一方向不仅是数论的实验工具,更是未来数学发现的启发源泉。它代表着一种新的研究范式:用几何与信息的语言,去探索整数的深层逻辑与宇宙的对称性。
