日本数学家错误阿贝尔数学奖伯源正树和森重文-小平邦彦-广平中佑-望月新一-深谷贤治-错误百出

伯源正树

森重文

小平邦彦
广平中佑

深谷贤治(邵逸夫奖2025)

演绎证明某事肯定是这样,演绎是从一般到特殊,只有演绎推理形式是必然有效的,因为大范畴的存在,是小范畴存在的充分条件,所以,演绎推理是必然的因果关系推理。
归纳说明某事在实际上是有效的,归纳是从一些特殊到一般。
溯因推理是说某事可能是这样。溯因推理是推理形式最弱的一种。
溯因推理借助不完全归纳预测成为一个命题叫做猜想(证明一个猜想是告诉你结果,让你按照规则找出原因-过程的必然性,把道理讲清楚)。
归纳只能预测,不能证明。
为什么?
我们证明一个数学命题就是一种整体上弱势溯因加归纳推理,每一个局部需要强势演绎推理。
为什么不能用归纳法证明?因为设立命题时使用少量样本归纳出来的,再用少量样本证明,就不可靠了。比如,你用10公斤力气把一块石头从高处扔到低处,再把这块石头从低处放回高处,10公斤力气就不够了。
举例哥德巴赫猜想:
原始信息(6=3+3,8=3+5,..。就是逐一归纳有限的样本,具有某种性质(两个素数之和),于是归纳推出“哥德巴赫猜想”推导出数量有无穷多个的样本也具有某种性质)。
在归纳基础上产生的猜想,通过演绎证明是不对等的,好比有倒钩的矛头,插入容易,取出难,无损伤取出不可能完成。
归纳是在一个有穷大的样本中逐一列举, 只要样本空间没有被穷尽, 使用的都是简单枚举归纳推理。
对于无穷大的样本, 我们根本不可能穷尽该样本空间, (例如哥德巴赫猜想中的偶数就有无穷多个)因此只能使用简单枚举归纳推理,简单枚举归纳推理是一种扩大前提的推理, 它的结论是不可靠的。
使用归纳推理提出假说, 其假说是非常脆弱的, 因为对它的证实是不可能的, 除非你穷尽样本空间, 而一旦如此, 你使用的已经不是归纳推理了。
它的脆弱性还表现在, 只要一个反例, 就可以容易地推翻这个假说。
无穷多个样本的数学定理必须是全称判断,数学家必须完成一个:由归纳出来的有限个事实样本去证实无穷多个元素的--不可能完全证实的命题进行演绎方法证明,并且结论是全称肯定判断的正确三段论只能是第一格的AAA式。这是绝大多数数学命题证明无法做到的。
溯因加归纳推理是从结果追溯原因的推理,溯因推理是关于采纳假说的推理.,采纳一个留待观察的假说不能被适当地称为归纳, 但它仍然是推理, 它的安全性低,成功率低,从逻辑规则说有一个大的障碍, 然而它是逻辑推导, 它仅以疑问的或猜测的方式断定其结论是真的。
因为它有一种完全明确的逻辑形式,归纳推理是基于有限观察的、从有限样本推出一般结论的推理, 它的前提是关于个别事物具有某种性质的论断, 结论却试图得出全体事物皆具有此性质的论断.。
不完全归纳出来的全称判断形成的待证命题,怎么可能通过演绎推理回到初始信息?让初始信息变成一个定理?
归纳产生的样本,推导出命题,归纳的样本没有进入命题因果关系;没有进入证据链,前提不是结论(即全称判断的命题)的必然原因,所以只能是猜测。
因为少量归纳产生的元素具有某种属性,夸大和膨胀了命题(有无穷多个元素),证明命题时候就要填补这个夸大的空缺。
伯源正树所有的证明都是归纳法,归纳假设:





森重文

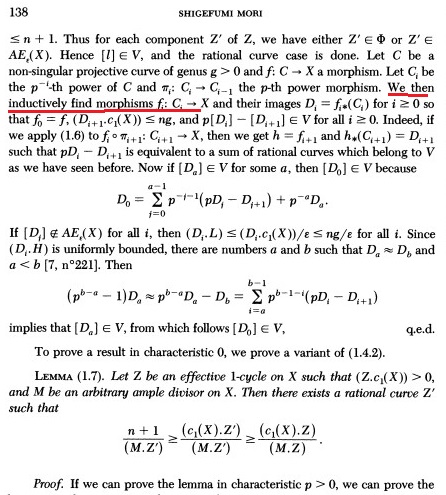
小平邦彦归纳法证明



其它内容乱七八糟,狗屁不通:
数学定理不能是或然判断。逻辑的本质就是必然得出。演绎推理的前提不能是或然判断的“估计”。
在这里必须是没有任何模糊性,而估计和假设就是模糊证明,论证中的一切推理应该井井有条,一切细节环环相扣。结论的正确性建立在前提的正确性和真实性基础上。
归纳假设证明和先验估计命题是数学家常犯的错误:
(1)没有进入因果关系;
(2)没有进入构成关系;
(3)无法被感知。
(4)估计和假设进入证据以后,如果从区分两类否定真理的角度来检视这一问题:
第一类涉及虚构或者主观创造的一些对象;
第二类涉及实际存在的对象。
而估计和假设的虚构的对象并不具有事务的全部属性。
(5)假设最后必须被证明才能进入证据链。
(6),假设理由的虚假性胡乱修改前提条件,得出错误结论。
(7),推理的无关性胡编乱造的结论不能算定理。
(8),隐含的假设性这些结论都有一个共同的缺陷,假设存在他们想要的内容,都是无关地联系他们预想的东西,例如张益唐和陈景润。
(9),论证的单一性这些论证都是违反演绎推理的基本规则,不能反推回去,正确的定理证明,百分之百可以倒推回去。




广平中佑的内容乱七八糟。使用归纳法证明,定理是多重假设。
(证明)设o是C在k上关于P的局部环,....。
我们将通过归纳...来证明这一点。......。
根据S的假设,....。
我们可以假设......。
由此可知,....。或者说,以P为中心的二次变换C‘满足我们定理中关于每个对应于P的点的假设


望月新一证明ABC猜想,归纳假设,估计
证明。首先,我们考虑断言(i)。.....过将k0替换为包含在ki中的k0的非分歧扩张,
我们可以不失一般性地假设....。这完成了断言(i)的证明。
接下来,我们考虑断言,对ni进行归纳。由于当ni = 0时断言(ii)直接由断言(i)得出,
我们可以假设ni≥1,并且断言...。
我们可以不失一般性地假设Gal(ki/k1)是一个p-群。
根据归纳假设可知,...。

深谷贤治归纳法
kenji fukaya

