那就来聊聊数学

戴榕菁

我知道在贾尼别科夫效应这个问题上，对于某些人来说，如果不聊聊数学，你就是让他看一万个视频他心里还是不踏实，毕竟这里涉及到了角动量守恒这个被认为是物理学基石的议题。那么咱们就来聊聊数学。下面是从维基上得到的对于贾尼别科夫效应的稳定性的数学分析的基本方程式【[1]】：

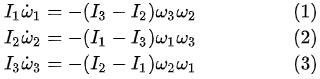
方程组（1，2，3）是著名的欧拉方程，其中I₁，I₂，I₃是物体的主惯性矩且被假设为

I₁ < I₂ < I₃

ω₁，ω₂，ω₃是沿着三个主轴方向的角速度分量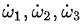，是三个主轴方向的角加速度分量。

他们的分析的第一步就是将上面方程组的(1)式对时间求导并将(3)式中的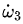代入求导的结果从而得到：

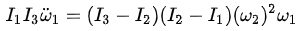(4)

因为I₁ < I₂ < I₃，所以(I₃ - I₂)( I₂ - I₁) > 0        

由(4)式他们得出结论说，只要一开始的时候ω₁有一个非常小的值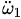，就有一个大于零的值，也就是说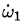会越来越大。

这里要注意这样两点：

1）欧拉方程组（1，2，3）的前提条件非常明确：没有外力。这使得我在前文“再聊聊贾尼别科夫效应”【[2]】中对于不存在外力的讨论显得多余了。

2）从前面的(4)式可以看出，这并不存在一个奇异点的问题，因而按照（4）我们是可以算出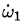的不断增大的值的。但是

3）我们再来看下面两个视频：

https://www.youtube.com/watch?v=Xrf1HzFJ8jc&t=27s

https://www.youtube.com/watch?v=1x5UiwEEvpQ

从上面两个视频可以明显看出的ω₁方向在来回的翻转中是不断变化的，也就是说不可能是沿着一个方向不断增大的。而(4)式中除了ω₁之外都被假设是不变的，因此只要ω₁的初始值大于零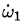，就总是大于零的。。。。由此可见，在太空站中的实际的贾尼别科夫效应运动与（1，2，3）方程组所描述的运动相去甚远！

讨论

对于满足于所谓的稳定性分析结果的人看了上述分析之后一定会说：(4)式样说明了物体沿着最小惯量轴的加速度会不断增大，从而会使ω₁大到能翻转的程度就行了，不必继续给出翻转后的运动是什么样的了。

但问题是，如果你相信欧拉方程可以准确地描述太空站中的贾尼别科夫效应运动，你有什么理由告诉我们物体的实际运动会不符合(4)式的描述？

其实，如果你说“太空站中的贾尼别科夫效应运动是在ω₁可以不断增大这点上满足欧拉方程，但是当物体开始翻转后的运动就不需要满足欧拉方程”，你等于在说太空站中的贾尼别科夫效应运动打破了角动量守恒----这是因为欧拉方程等价于角动量守恒。。。。如果你没有特殊的理由（诸如假设运动可以不满足角动量守恒这样的理由），你就不能说ω₁大到一定程度之后就可以不满足欧拉方程了。

现在想想，也难怪被西方誉为当代最伟大的数学家之一的陶哲轩会用内力来解释太空站中的贾尼别科夫效应运动的总角动量的变化。。。。其实，本文所引用的据说是已经有将近两百年历史的分析其实质就是用内力来解释----因为它的出发点就是假设没有外力。

但是，我们知道牛顿定律的最基本的一个结论就是在没有外力的前提下，物体的总角动量是不会变的。

欧拉方程是我在北航读大学时的理论力学课上学习的（那时候贾尼别科夫还没有发现他的效应呢），刚才为了写这篇文章又重新复习了一遍它的推导，并没有发现什么问题。。。。当然，以大数学家欧拉的名头来说，我们似乎也不应该怀疑它有什么问题。

但另一方面，本博客之所以如此地要在太空站中的贾尼别科夫效应运动这个问题上冒触犯角动量守恒之大不韪而固执地叫真，最主要的是因为实在无法从任何现有的视频中看出在物体翻转过程中的总角动量可以在任何意义上等价于最初的角动量。。。。

不论你如何强调只要最初有一点点沿最小惯量轴的角速度，欧拉方程就能让它变得很大，哪怕你说破了天，只要你的前提假设是没有外力矩，那么在包括翻转在内的整个运动过程中总角动量就不能变！！！因为只要它一变就打破角动量守恒！

但是，你们谁能看出下面这个视频中的总角动量是守恒的：（？？？）

https://www.youtube.com/watch?v=Xrf1HzFJ8jc&t=27s

其中最明显的一点是在沿着中间惯量轴的转动方向相同大小基本相同的前提下，沿着最小惯量轴的翻转方向可以一会儿保持不变一会儿完全相反，根本没有定数-----这根本不可能保持总角动量不变！！！

结束语

前面提到，现有的用欧拉方程来对贾尼别科夫效应运动进行的所谓的稳定性分析的前提都是没有外力作用。在这样的前提下他们居然可以完全不顾所有来自太空站的明显不满足总角动量守恒的现象而盲目满足于“稳定性”这个大名词带给他们的安全感。

但另一方面，人们假定太空站里的贾尼别科夫效应运动没有受到任何外力作用是一回事，而太空站里面到底是否实际上有可以影响贾尼别科夫效应运动的外力又是另一回事。从这个意义上来说，我在前文“再聊聊贾尼别科夫效应”【2】关于太空站中是否可能有实际上会影响贾尼别科夫效应运动的作用力的讨论就很有意义了。

这里再针对太空站里是否会有影响贾尼别科夫效应运动的外力这个问题多说几句。

如同在大气层内的物体在空中的运动一样，我们首先要考察的就是两种力：重力和空气作用力。

由于太空站内处于微重力环境，如我们从视频上看到的，重力的影响可以直接忽略，这一点我在“再聊聊贾尼别科夫效应”也讨论过了。至于空气作用力，既然人能够在里面生存，那就一定会有空气作用力。但是，了解空气动力学的人都知道，空气对于太空站内的物体的作用力属于是阻力，而且在这种低雷诺数的范围里可以引起局部振动的湍流都不会有，因而不具有可以让物体做来回周期性翻转的能力。所以空气的影响也可以被忽略。那么是否存在其它的诸如电磁力之类的隐形作用力呢？这一点就回到我在“再聊聊贾尼别科夫效应”一文中的论点，从视频中的贾尼别科夫效应运动的周期性翻转特性来看，我们也可以否定它们是由电磁力这样的隐形作用力造成的可能。

所以，除非有什么我们人类目前还不知的自然力在起作用，通过我最近几篇文章的讨论，我们可以相当确定地说：太空站里的贾尼别科夫效应运动打破了角动量守恒定律！！！

现在我们实际上面临着这样两个层次上的问题：

1）为什么会出现角动量明显不守恒的现象？

2）为什么Pointsot简化了的欧拉方程会得出角动量不守恒的结果？

这是两个不同层次的问题，彼此之间不一定有着必然的联系。比如说，假如从角动量守恒出发的欧拉方程的推导或Pointsot对欧拉方程的运用中存在问题，那么上面就是两个完全不同性质的问题。。。。但是，如果欧拉方程的推导没有问题而且Pointsot对欧拉方程运用也没有问题的话，那么上面就是两个彼此关联的问题了。

相关链接：

再聊聊贾尼别科夫效应

难道被苏联封了40年的真正秘密是。。。？

-------------------------

[[1]] Wikipedia. Tennis racket theorem. Retrieved from: https://en.wikipedia.org/wiki/Tennis_racket_theorem. Last edited on 29 November 2024, at 06:27 (UTC).

【[2]】戴榕菁（2025）再聊聊贾尼别科夫效应