戏剧性的薛定谔

戴榕菁

相对论出问题了，尤其是狭义相对论彻底错了（参见【[1],[2],[3]】）。尽管主流物理学界还硬挺着不承认这一点，但是很多场合下的口风的改变表明他们正在痛苦的思考如何吞下这颗苦果----这颗苦果不容易消化，它将让一大把的诺贝尔奖的颜色看上去不那么鲜艳不说，关键是怎么再去圆相关的理论。

在受到狭义相对论的错误冲击最大的量子理论领域，薛定谔方程似乎是极少数不受狭义相对论的错误影响的理论，因为薛定谔在发布他那获奖方程的文章中明确表示，他不认为狭义相对论适用于他所讨论的量子力学问题，所以他不打算象德布罗意那样地去用狭义相对论进行推导。从这个意义上说，薛定谔似乎应该是所谓的现代物理学中最幸运的一个人。但或许是因为他看起来特立独行，他也是现代物理学中极具戏剧性的一个人。

明明薛定谔的推导是针对微观粒子的动力状态，哥本哈根学派硬是将它解释为针对粒子在时空中存在概率。薛定谔不服，于是造了一只猫用以说明哥本哈根派的概率说之荒唐，结果不但他那只猫被哥本哈根派毫不客气地收归己有作为说明概率说的一个经典，而且由此衍生出涉及到冯诺伊曼和维格纳等数学界和物理学界的大卡们的量子理论中与薛定谔猫有关的一堆理论【[4]】，甚至还整出了那个平行宇宙的理论。。。。唯一的问题是所有这些理论都违背了薛定谔的本意。

比所有上述这些更为戏剧性的当属薛定谔自己对他那著名方程的推导了。两年前，出于好奇我试图找到薛定谔方程的推导，结果发现了各路科普人士给出的各种有关薛定谔方程推导的故事或说法。有的人说薛定谔方程就是由能量守恒直接得出的；还有不止一专业物理人士在Quora上声称薛定谔方程是凑出来的，因为那是不可能推导出来的。最牛的是YouTube的某来自澳大利亚的知名女科普网红（专业物理人士）专门做了关于薛定谔方程的视频，说有一位教授让薛定谔整出波函数的方程，薛定谔说没问题；于是他辞别妻子与几个美女在一偏僻风景区呆了两个月之后，就整出了那个著名的方程，但在他发表的文章中根本就没有严谨的推导。

我当时感觉很难相信他们所给出的解释也罢故事也罢，毕竟薛定谔的那个方程不但获得了诺贝尔奖，更是整个量子力学的最最基础的内容。直到我找到了薛定谔1926年发表在Physics Review上的那篇获得诺贝尔奖的原文也就是上面提到的视频中显示的那篇文章【[5]】并认真研读之后，我才明白了那些有关薛定谔方程推导的评论或故事的用意了。下面我们来一起走一遍薛定谔是怎么推导他的方程的，看看你们是否会和我的看法一致。

一．薛定谔的推导

1. 前提条件和关键步骤

薛定谔首先指出他的推导的前提条件是微观粒子的运动具有德布罗意所说的波动性以及传统力学所研究的粒子性，从而具有波动和粒子二重特性。

他的出发点是考察一个虚拟的质点受到势能为V(x, y, z)之保守力的作用，在位形空间（configuration space）q-空间 （q-space not pq-space）中运动。其动能可以表达为：

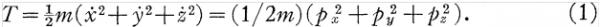
接下来他说：

著名的哈密尔顿的作用函数W，

作为一个（积分的）上限t和坐标x, y, z的终点值的函数它满足哈密尔顿偏微分方程，

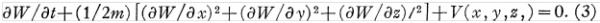
上面关于（2）和（3）的这两段话很关键，所以我尽量按照原文来翻译，其中（积分的）是我根据原文明显暗指的意思加进去的。（3）式中的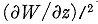的多余的斜杠应该是当年打字时的输入错误。

为了读懂上面这段对于全文来说非常关键的两段话，我认真地复习了一把哈密尔顿偏微分方程，但根本找不出（3）式这种形式的哈密尔顿偏微分方程。

然后我就试着用V(x, y, z)和(1),(2)式来推导出(3)，可是怎么也得不出被薛定谔称之为哈密尔顿偏微分方程的(3)式。后来我决定将最简单的引力场中单个质点的自由落体运动带入(1),(2),(3)式看看，结果发现(3)式连最简单的单个质点在引力场中的自由落体运动都不满足！难道这就是我根本推导不出(3)式来的原因？？？

这里恳请感兴趣的具有数学或物理学背景的读者自己去推导一下（3）式，或者用诸如简单自由落体之类的例子来验证一下（3）式的正确性，看看是否能推出（3）。如果有谁严格推出（3）式，那么他就能给出薛定谔方程的严格推导了。如果有人如我一样发现（3）根本连最基本的质点在重力场中自由落体运动都不满足的话，那么我们就一起发现了20世纪物理学的又一大毛病：薛定谔方程的推导至少是部分地有问题。

2. 比较正常的推导步骤和讨论

虽然从（1）到（3）仅有短短的几行，却是整篇文章中非常关键的几行。有了（3）式之后，接下来的内容虽然仍是一地鸡毛，但相对于连最简单的单个质点在引力场中的自由落体运动都不能满足的（3）来说属于比较正常的推导和讨论了。 当然，考虑到薛定谔这篇文章在整个近代物理学中的地位，我这里再次声明：我自己发现（3）连最简单的单个质点在引力场中的自由落体运动都不能满足，但我不排除别人可能发现其实（3）没问题的可能性，所以欢迎更多的人来验证（3）式。

2.1 （3）式的解

为了求解（3）式，薛定谔取

薛定谔将E称为总能量，是一个常数，S是x, y, z的函数。

这里又有问题了：如果E是总能量，那么我们应该有E = T + V，从（4）我们就应该有：

?W/?t = ? (T + V )

但是，根据（2）我们应该有?W/?t = T - V。

我曾想过一种可能是（2）的减号其实应该是加号。一般来说人们将T - V称为拉格朗日函数，而将T + V称为哈密尔顿函数。既然薛定谔这里将（2）的函数称为哈密尔顿函数，或许那里的减号是在将1926年的纸质杂志转为电子版时AI出了点小错误。但又一想，还是不对，即便把（2）的减号改为加号，我们得到的也只是?W/?t = （T + V ）而不是?W/?t = ? (T + V )。假如我们在（2）的积分号前面加一个负号并将T – V改为T + V，这似乎就可以解决这里的问题，但是等到后面的（7）式时那个负号又会出问题。总之，他选（4）作为（3）的解，并将其中的E说成是总能量会造成一些列的自相矛盾的问题。

如果读者认同我上面的分析，那么到这一步时我们已经面临了这样两个问题：

1）（3）式本身有缺陷，我不但用（1）和（2）推出的结果与（3）相去甚远，而且用最简单的质点运动发现（3）是不正确的。

2）即便假设（3）是正确的，选用（4）作为（3）的解且声称其中的E为总能量就会带来一系列的逻辑困境。尽管（4）的选用是教科书上作为求解哈密尔顿的偏微分方程的标准形式，但（3）并不是哈密尔顿的偏微分方程的标准形式。

有哪位数学专业的或物理专业的可以在这里提供一些专业性见解？

先把问题放在这里，我们接着往下看。

将（4）代入（3）得到：

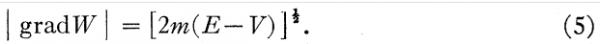
接下来薛定谔给出了（5）的几何解释：

对于任意一个给定的时刻t，空间中的任意一个函数W可以表达为一组其值为W的值（例如W₀）的曲面。但另一方面，我们可以从W₀开始任意一组其值为W的空间曲面来得到（5）式的解。这是因为我们只要假设W₀的某一边的W值为正，在W₀上的这一边的每一点的法线上取长度为：

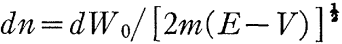
这样得到的所有的点的值显然是W₀+dW₀。依次下去便可得到在给定的t瞬间的所要的整个曲面系统。

由（4）可以看出，当时间改变时，上述曲面系统是不变，只是W的值沿着曲面的法向以下面的速度传播：

这个速度u是总能量E和V(x, y, z)的函数。

这里薛定谔应该是用u = dn/dt 得出（6）的，只不过他把负号略去了，因为u只是相速度。

相应地，我们也可将上述的体系看成是具有W值的曲面在空间沿着各自的法线以（6）式的速度u运动。这样我们就可以得到各向同性但非均匀的光学介质中的稳定波，W正比于相位而u就是相速度（介质的折射率需要正比于u^-1）。他说上述的构造显然等价于惠更斯原理。

薛定谔接下来说，对于质点来说，正如众所周知的：

（y 和 z方向也一样）。

这个（7）也是问题重重。从（2）出发，我们会得到?W/?x = m? - ?V/?x + 常数，这显然与（7）不符。这里又回到前面的（3）式的正确性和（4）式中的E是否为总能量的问题了。假如（3）式是正确的而（4）中的E确实为总能量，那么（7）就成立，否则（7）就不成立。反过来说，假如（7）成立，而（4）式的E确实是总能量，那么（3）一定成立。

如果有人能够证明（3）或（7）成立，那么他就已经严格地推导了薛定谔方程（当然，这里指的是没有被哥本哈根修正过的原始方程），他就可以站出来理直气壮地批驳那些所谓的薛定谔方程无法推导的言论，可以去帮助改写教科书。反过来说，假如有人如我一样认为（7）有问题，那么我们就一起站在了认为薛定谔方程推导有问题的行列中了。

再次欢迎数学专业和物理专业的读者来这个地方提供专业性见解：（3）和（7）到底是否严格成立？

我们再接着往下看薛定谔的文章。

给出（7）式后，薛定谔解释说，前面提到的相速度u不是质点的速度，质点的速度由（7）和（5）给出：

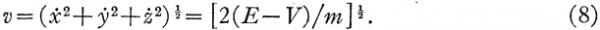
他指出，对比（6）和（8），u和v具有反比的关系，这意味着对应于哈密尔顿的力学原理于对应于费马的光学原理就联系在一起了。

2.2. 关于光（波）与粒（子）的关系的历史回顾

在这一节里，薛定谔将力学与光学做对比，指出当光经过曲率半径很小的物体表面时，几何光学已不再适用，那时我们必须要用波动光学，与之相应地，在很小的空间范围内，普通力学就不再适用，我们必须要借用波动的概念来研究粒子的运动。

2.3. 求解方程（4）

在论证了普通力学不再适用于微观世界之后，薛定谔开始求解（4）式。

他假设（4）式的解为：

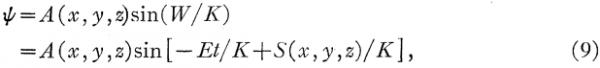
其中ψ 为波函数，A为振幅函数。因为sine的自变数必须是纯数值，所以常数K不可缺少并具有作用（能量×时间）的量纲。（9）式的频率显然是：

我们难以抗拒将K看成是普实常数的诱惑，因为假如K等于h/2π，那么频率ν就等于

h是普朗克常数。这里他说，著名的能量与频率之间的关系就这样非常自然而不需借助任何外力地被推导出来了。

哇，难道这家伙要挑战爱因斯坦？（11）式可是让爱因斯坦获得诺贝尔奖的式子。爱因斯坦在1905年提出该式，1921年获诺贝尔奖。薛定谔这家伙在1926年声称很自然地推导出了（11）式，至少也应在文中这个地方向爱因斯坦致敬才是呀J，呵呵。

接下来薛定谔开始向相对论发起第一波非正式的挑战：

他说在普通力学中，绝对能量是没有意义的，人们只关心能量差，所以人们用相对论的方法以及质能等效的概念来解决那个问题绝对能量的问题；但是在他这里，这种借助相对论的做法是完全没有必要的。这是因为（10）式与（11）式中的波动频率ν依赖于零点能量，而它们的波长不依赖于零点能量，而波长比频率更重要。由（11）和（6）得出波长公式：

他说E – V 是动能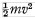所以独立于总能量的零点值。将动能代入（12）我们得到：

这家伙在这里应该向他的偶像德布罗意王子致敬呀J。不过不要紧，因为正是在这个地方与德布罗意的解的一样不但让薛定谔的解之凑出来而不是严格推导出来的特性在近一百年后难以掩盖地显露出来了而且暴露出薛定谔其实根本没有认真阅读他的偶像德布罗意王子对于所谓物质波长公式的推导！这是因为在2023年戴某人详细地指出了对于狭义相对论的应用如何导致了德布罗意的公式错误以及如何修正德布罗意的公式，即这里的公式（13）。在后面的第2.10节（即薛文的第10节）我们会看到薛定谔明确表示相对论不适用于他的理论，所以他在推导中没有用相对论。当初没有想到的是假如他的解不是直接凑出来的而是严格推导出来的，他就根本的不出（13）式样来，因为如戴某人一步步地指出的【[6],[7]】德布罗意之所以会得出（13）是因为用到了相对论，只要他不用到相对论，结果就完全不一样。既然薛定谔没有用到相对论，如果不是他照猫画虎地模仿德布罗意的解凑出自己的解来，他根本不应该得到（13）式!这也间接地告诉我们为什么（3）连最简单的单个质点在引力场中的自由落体运动都无法满足的原因：那不是严格推导出的，而凑出来的！而（3）式的错误决定了（7）式不可能对！我在前面提到因为薛定谔在推导方程的过程中没有用的相对论，所以薛定谔方程似乎是量子力学中少数甚至唯一一个不受狭义相对论影响的理论。但是，从（13）可以看出，非常遗憾地，由于薛定谔在凑出（3）式和（4）的过程中试图与德布罗意的解在形式上一致，他其实已经间接地受到相对论的影响了！

接下来薛定谔将波长λ与原子量级的尺度a进行比较：

他说当λ/a为一的量级时，普通力学就没意义了。

接下来他论证了粒子速度v其实就是按照他的波动力学得出波包的速度，也就是群速度。他还说，波包重心的轨迹和普通力学中的粒子轨迹是一样的，即便当轨道的尺度没有波长大的时候也一样，只不过那时波包本身就已经超出了轨道了（本文注：应该说这时波包已经覆盖了轨道）。

2.4. 推导薛定谔方程并求解

在这一节里薛定谔开始推导他的那个诺贝尔得奖方程了。

他首先用普通的波动方程来考察单个质点在外界力场中的运动：

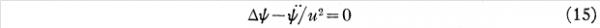
将（6）式代入（15）的u中，并指出这一代入对于ψ的影响是通过因子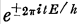的。所以得到：

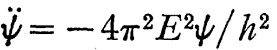
将上式与（6）代入（15）：

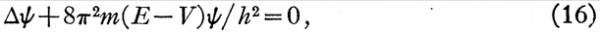
其中ψ被假设为只依赖于下x, y, z。

（16）就是著名的薛定谔方程的最原始的形式，所有的现代版本（包括他这篇文章后面的（26）式和（32）式）都是从这个方程衍生出来的。没有人独立地从最基本的力学直接推出今天的通用版本。所以，如果有人严格证明前面的（3）或（7），他就等于严格证明了今天所有的版本。如果有人能证明（3）或（7）有问题，那么他就证明了今天所有的版本都有问题。

接下来薛定谔就要给（16）求解并讨论它们的意义了。

首先考虑电场势能的情况。取

e = 电荷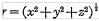，，所以对于简化的氢原子问题：

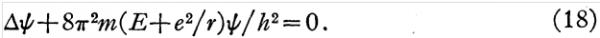
在全空间都连续的有限单值的解需要满足下述条件：

上面的第一组解是普通力学中的抛物线轨道运动，第二组解对应着玻尔的稳定能级的椭圆轨道运动。

他说：虽然他这里不对上述结论进行冗长的证明，我们可以用三维的极坐标令ψ为极坐标的函数和半径的函数之积来求解，所得到的解为对应于方位量子数 （azimuthal quantum number）的球面调和函数和有着有限数目的正根的类似Bessel函数r的函数之积，而这里的正根的数目正好是玻尔的轨道数。当r增加超过最后一个最大或最小根之后，那个函数就以指数下降。所以整个波动现象，尽管在数学上延申到整个空间，实际上只局限在几埃米的直径范围内，这就是波动力学的“原子”。上述解中的任何一个都极其类似弹性球面振动，都具有（1）球面，（2）锥面，（3）平面的“结面（node surfaces）”。但是我们不应把构成原子的一般波动看成是仅限于这些解中的某一个，它们的分离很大程度上取决于坐标的选取。

这里薛定谔还加了一个注：不能象普通力学那样将问题局限在2维运动，因为波动现象基本上是三维的。

薛定谔指出：对应于E的每一个离散值，都是一个特殊解，将这些解用任意常数进行线性叠加可得到（18）的对于给定E的一般解。其中任意常数的数目正好等于相应能级的“统计权重”，或者说等于在扰动力（perturbing forces）作用下根据玻尔的理论（以及薛定谔自己的理论）得到的能级的数目，这样就不需要相关问题的所谓的简并（degeneration）了。他说普通量子理论中的能级数不一定是正确的。

他接着说，确定的实验证据迫使我们要排除那些具有零赤道量子数（equatorial quantum number）的能级，而可喜的是按照这个新的理论，所得到的简并能级或频率数从一开始就是正确的。这个理论不需要任何其它的补充，因为它已经排除了对应玻尔轨道的零赤道量子数的解。

结束这一节讨论前，他指出，对应着原子的正常状态的最低的能级或者说对应着波动的“基频”，只有一个振动模式，一个非常简单的模式，它的波函数完全是球面对称，没有任何结面（node surface）。径向量子数以及球面调和数都消失了。

2.5. （18）式只对有限个E值具有有限解的原因

这一节的讨论我这里不赘述，感兴趣的读者自己去看吧。

2.6. 关于几个特殊解的讨论

调和振动问题，与普通量子理论的nhν₀不同，这个新力学的解为

转子问题：

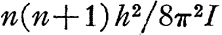
（I = 惯性矩），那个原来著名的n²由n（n+1）取代了。对于我们所感兴趣的能级差来说，这相当于用(n+1/2)²取代n²，因为

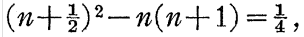
独立于n。众所周知，半量子数是得到多数简单带状频谱的实验支持的，或许没有任何实验与之相悖。接着他说为他提供了很多帮助的洛克菲勒学院的Fues先生发展出了一种比普通力学中的摄动法简单的多却可以得到基本一样的结果的摄动法用来解（16）式。他介绍了用Fues的方法解决的某个特例。

他又说他用相关方法得出的某些解与海森堡，波恩和乔丹用矩阵理论得出的结果在数学上完全一致。

2.7. 用哈密尔顿原理推导更一般形式的薛定谔方程

我刚读到这一节的开场白时还以为或许这一节可以解答我前面提出的有关（3）与（7）的疑惑了。但非常失望地发现，与上面的推导相比，薛定谔的这一节可以说是在玩抽象艺术。他的这一节根本没有给出推导，只是说他得出了某种结果，并从该结果可以进一步看出其它结果。

考虑到他在前面几节的系统推导中存在的至少在我目前看来是错误的地方，我完全无法在自己能够按照他所提供的思路来推出他所声称的结果之前相信他这一节的所声称的结果的正确性。但另一方面，它这一节提供的思路过于抽象，其过程跳跃性大而结果繁复，再说如果（3）或（7）确实错了，那么凭什么认为在用简单明确的方法都推不出正确结果之后用更为复杂抽象的思路就变好了呢？所以，至少现在我是懒得再花时间去一步步地跟踪他这一章的逻辑了。

在这一节里他跳跃性地给出的比他（16）式在形式上更具一般性的（26）式如下：

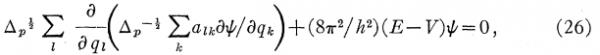
平心而论我不认为这种在广义坐标系中一般性的表达形式有什么特殊意义，至少近一百年后的今天的教科书通常用的都还是在(x, y, z)坐标系中的薛定谔方程。

他在同一篇文章里，在相隔了大半篇文章的两节中用两种不同的思路来给出基本上来说是同一个方程，这让我感到他内心对于这两种方法的哪一种方法都没有十分的把握。

另一方面，如果这一节的思路是正确的，那么为什么近一百年后的今天，人们仍然认为薛定谔方程不是推导出来的，为什么教课书上不坦然地介绍这个原汁原味的推导思路呢？

感兴趣的读者可以自己按照他这一节的内容去推导一下（26）。如果这一节提供的思路可以有效而且正确地得到（26），并有效正确地从（26）得出（16），那么即便是（3）或（7）有问题也不重要了，毕竟得诺贝尔奖的是（16）和（26）式，而不是（3）或（7）。同样地，假如有谁能看出他在这一节的推导有逻辑错误的话，那么就又一次抓到20世纪物理学在最最基本的理论基础上存在的一个漏洞了。

2.8.波函数ψ的真实物理意义

（16）或（26）中的波函数ψ只依赖于空间坐标，对时间的依赖是通过对应不同的E = E_l的实数部分（real part）发生的：

其中θ_l是相位常数。所以，如果u_l（l = 1, 2, 3 ….）为特征函数，那么波动问题的最一般的解（实数部分）将是：

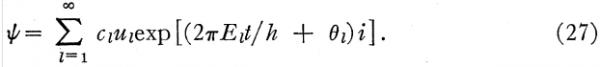
（为简便起见，薛定谔假设所有的特征值都是单值和离散的）。c_l都是实数。复数函数ψ的绝对值的平方为：

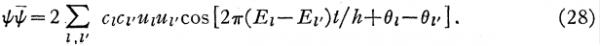
其中头上带一横的是ψ的共轭复数。

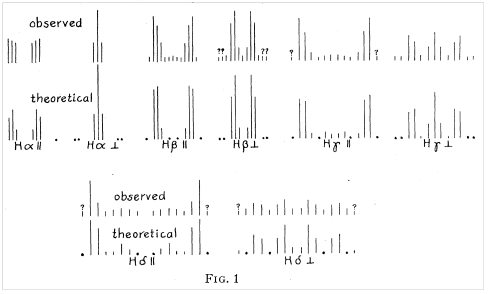
薛定谔指出，一般来说，ψ和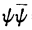都是广义坐标q₁ … q_N和时间的函数，这使得理解ψ的物理意义造成困难，但是对于氢原子来说，这一点困难不存在了，因为这时可以基于下面这个假说来相当正确地计算诸如斯塔克效应分量（Stark Effect component）[[8]]的密度（见图1）：

电子的电荷并非集中在某一点上，而是分布在整个空间上，而它们的分布正比于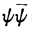

。

他接着指出，即便有上述的假说，电荷仍然只是集中在几个埃米的区域内，与原子核的距离超出了这个区域后，ψ的就迅速趋于零。电荷的脉动由对于氢原子的（28）的特殊形式控制。为了计算辐射，需要将（28）分别乘以x, y, z然后对整个空间进行积分，例如：

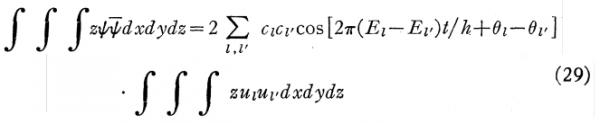
因此，电力矩是偶极子的叠加，它们对应着以频率

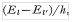
振动的特征函数对。对应于某一特定频率的辐射正比下式的平方：

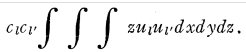
在又经过了一番讨论后，薛定谔提出了关于波函数ψ物理意义的下述更为一般的假说：

电荷的连续分割（continuous partition of the charge）是相应点电荷模型所有可能构型的连续多重构型的某种平均值，该平均值在构型空间中以量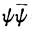作为某种权重函数。

薛定谔指出，在氢原子的情况下，上述假说就退化为前面提到的那个更简单的假说。

2.9.薛定谔方程的更一般表达式

在这一节中，薛定谔并没有象在前面2.7节中那样重新推导出一个更一般的薛定谔方程表达式（26），而是仅仅在（16）和（26）的基础上给出了更为一般的形式（32）：

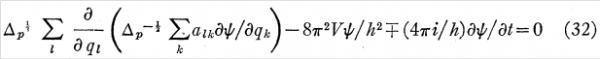
他说因为波函数的物理意义体现在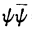上而不是单一的ψ上，所以（32）式中取加号或减号都无所谓。

接下来他讨论了（32）式中的V为非保守势能的情况，特别是由一束入射光造成的非保守势能的情况。

2.10. 薛定谔对文章的结束语

首先，他指出该文没有用到相对论也没有涉及磁场力。他给出了他的理由：首先，相对论还没有被推广到多于一个电子的系统。第二，有关氢原子的相对论理论显然是不完整的，因为它们的结果与实验结果之间有着严重（grave）的矛盾。他给出了一个例子。

二. 本文结束语

1）为了方便读者在阅读本文时对照薛定谔的原文【5】，本文从2.2节开始的第2.X节对应的是薛定谔原文的第X节。

2） 今天市面上大家一致认为薛定谔方程不是推出来的而是凑出来的；在本文开头提到的那个说薛定谔在度假村里嗨了两个月后发表了薛定谔方程时没有给出推导的视频【[9]】中，那个网红还提到费曼在对薛定谔方程的推导进行评论时也指出薛定谔的文章用的是启发式（Heuristic）的推导而没有给出严格推导，而且用了错误的论点，费曼还说没人能推出薛定谔方程，但只要它正确就行。

但是，通过本文的讨论我们可以看出如果说薛定谔在得出他的方程的过程中完全没有进行推导的话，那一方面是对于薛定谔原文过于苛刻不够公平，但另一方面却似乎是在故意袒护薛定谔。

应该说在2.7节（即原文的第7节）之前薛定谔所给出的推导和论证与任何其它物理文章中的推导和论证相比，其在细节上并没有过分的跳跃。不论是一百年前的物理学文章还是今天的物理学文章，都不可能象老师在课堂上那样一步步地给出推导，而是要读者自己去完成很多具体的细节性推导。当然，薛定谔的2.7节可以说是完全没有给推导，只是跳跃性地给出部分思路加上他的看似直觉性的判断，最后得出结果，只不过如果因为薛定谔在他的第7节（本文2.7节）的跳跃性就说薛定谔整篇文章都没有推导，对于薛定谔来说是有失公允的。

但另一方面，费曼说薛定谔用了某些错误的论点又象是在故意袒护薛定谔。根据我的推导，我个人认为他的（3）式和（7）式是错误的！错误的式子与错误的论点在错误程度上是不同的！错误的论点可以是在讨论时说错的话，而错误的式子则是数学结果的错误！

相应地，薛定谔的主要问题不在于人们所说的他的跳跃（尽管这对于第7节是个严重的问题），而恰恰是他在第7节以前没有怎么跳跃！---- 这里的逻辑很简单：两个独立的错误有时可以相互抵消而得到正确的结果。。。。但如果结论B是由结论A按照正常的逻辑推理在没有发生严重跳跃的前提下得出的，而结论A本身是错误的话，那么一般会认为结论B也是错的----至少在中学课堂里老师都是这么教的！

3）说回到薛定谔在第7节以前的推导，其思路也确实比较奇怪。他从简单质点的运动出发，通过类比得出波动方程。这应该就是费曼说薛定谔的推导是启发式（Heuristic）的推导的原因。但其实，如果逻辑严格，Heuristic未必就不行，否则物理学恐怕就要倒闭了。所以，薛定谔的问题不在于是否Heuristic，而在于他的逻辑是否有错误！可见，费曼表面上批评薛定谔，骨子里却在避重就轻地袒护他。

4）从本文可以看出，薛定谔与哥本哈根的主要区别在于：薛定谔认为波函数代表的是粒子电荷密度的分布，而哥本哈根认为波函数代表的是粒子出现的几率。其实，两者都存在着逻辑缺陷。

一方面，迄今为止，哥本哈根派也无法满意地解释由薛定谔的那只猫引出的所谓量子力学测量问题；而如我之前指出的【[10],[11]】，薛定谔的那只猫本身就存在着逻辑缺陷。另一方面，按照本文给出的图1，薛定谔所说的电荷分布密度的假说其实是有一定实验依据的。而波恩提出的几率说，更像是一种纯思辨。

几十年后的所谓单个电子的双缝实验似乎支持波恩的几率说而不利于薛定谔的电荷分布密度说。但实际上，我们只能说单个电子的双缝实验更接近波恩的几率假说而不接近薛定谔的电荷分布密度说，而不能说它就验证了波恩的几率假说。

5）至于费曼说薛定谔方程正确地反映自然这一点嘛，或许最多也只能说是在一定程度上反映自然吧。至少薛定谔按照他的理论得出德布罗意波长这一点就暴露出他的方程只能是近似地正确。

总之，现在看来量子力学从根上就存在问题。那个费曼的理论还存在着需要进行重整化的能量奇点问题，至少薛定谔的方程还没有这个问题。

【[1]】戴榕菁 （2024）广义相对论之对与错

【[2]】戴榕菁 （2024）当哲学被藐视之后正式出版之意义

【[3]】戴榕菁 （2024）当哲学被藐视之后。。。。（2024版）

[[4]] Wikipedia. “Schr?dinger's cat”. Retrieved from: https://en.wikipedia.org/wiki/Schr%C3%B6dinger%27s_cat. Last edited on 27 June 2024, at 03:27 (UTC). 

[[5]] Schr?dinger, E. (1926). “An Undulatory Theory of the Mechanics of Atoms and Molecules”, The Physical Review, Vol. 28, No. 6,  December, 1926. Retrieved from: https://web.archive.org/web/20081217040121/http://home.tiscali.nl/physis/HistoricPaper/Schroedinger/Schroedinger1926c.pdf

【[6]】戴榕菁 （2023） 德布罗意波之错和薛定谔之幸运

[[7]] Dai, R. (2023). Correction to de Broglie Wavelength. Retrieved from: https://www.academia.edu/111922499/Correction_to_de_Broglie_Wavelength

[[8]] Wikipedia. Stark effect. Retrieved from: https://en.wikipedia.org/wiki/Stark_effect. Last edited on 30 October 2023, at 16:57 (UTC).

[[9]] Up and Atom. (2019-12-12). [YouTube] What is The Quantum Wave Function, Exactly? [video] url: https://www.youtube.com/watch?v=EmNQuK-E0kI&t=9m22s

【[10]】戴榕菁（2023.6）薛定谔猫的跳跃

[[11]]Dai, R. (2023). “The Genetic Defect of Schr?dinger's Cat”. Retrieved from: https://www.academia.edu/104037882/The_Genetic_Defect_of_Schr%C3%B6dingers_Cat