触类旁通的全美数学竞赛

发表时间：2023-12-11 11:44

2023-12-11

最近在辅导几个小孩做数学竞赛题，临时抱佛脚，参看了历代AMC8 的考试题。发现在AMC数学竞赛的考题中，有很多类似的数学题，是可以触类旁通，举一反三的。例如2018年的AMC8数学竞赛中的第二题：

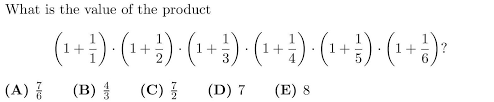
和2006年的AMC8 全美数学竞赛中的第九题，实在就是同一道题：

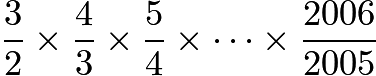
再看1985年AJHSME全美初中数学竞赛中的第九题，也基本上是大差不差：

images (1).png

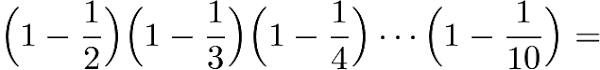
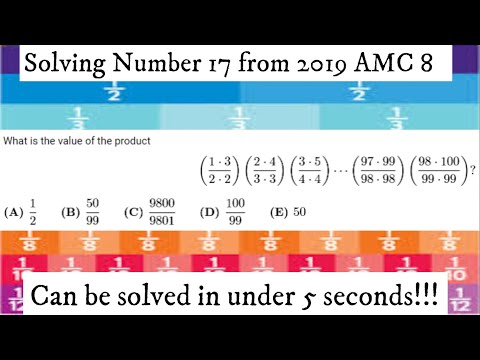
再看2019年AMC8全美数学竞赛中的第十七题，简直就是一个送分的傻瓜题：

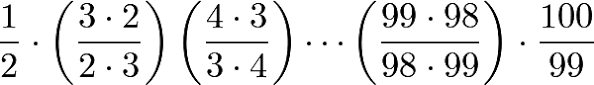
那么再看第2022年AMC8全美数学竞赛的第八题，是不是简直就弱爆了：

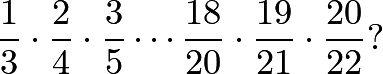
还是在2018年，AMS8全美数学竞赛的第五题：

What is the value of $1+3+5+\cdots+2017+2019-2-4-6-\cdots-2016-2018$ ?

$\textbf{(A) }-1010\qquad\textbf{(B) }-1009\qquad\textbf{(C) }1008\qquad\textbf{(D) }1009\qquad \textbf{(E) }1010$

和1990年全美初中数学竞赛第十六题，也似曾相识：

$1990-1980+1970-1960+\cdots -20+10 =$

$\text{(A)}\ -990 \qquad \text{(B)}\ -10 \qquad \text{(C)}\ 990 \qquad \text{(D)}\ 1000 \qquad \text{(E)}\ 1990$

还有1993年全美初中生数学竞赛第19题：

$(1901+1902+1903+\cdots + 1993) - (101+102+103+\cdots + 193) =$

$\text{(A)}\ 167,400 \qquad \text{(B)}\ 172,050 \qquad \text{(C)}\ 181,071 \qquad \text{(D)}\ 199,300 \qquad \text{(E)}\ 362,142$

1996年全美初中数学竞赛第12题：

$1-2-3+4+5-6-7+8+9-10-11+\cdots + 1992+1993-1994-1995+1996=$

$\text{(A)}\ -998 \qquad \text{(B)}\ -1 \qquad \text{(C)}\ 0 \qquad \text{(D)}\ 1 \qquad \text{(E)}\ 998$

2013年AMC8数学竞赛第三题：

What is the value of $4 \cdot (-1+2-3+4-5+6-7+\cdots+1000)$ ?

$\textbf{(A)}\ -10 \qquad \textbf{(B)}\ 0 \qquad \textbf{(C)}\ 1 \qquad \textbf{(D)}\ 500 \qquad \textbf{(E)}\ 2000$

2017年AMC8全美数学竞赛的第八题：

Find the value of the expression $100-98+96-94+92-90+\cdots+8-6+4-2.$ $\textbf{(A) }20\qquad\textbf{(B) }40\qquad\textbf{(C) }50\qquad\textbf{(D) }80\qquad \textbf{(E) }100$

尤其是令人惊讶的是，2018年AMC8全美数学竞赛的第15题：

In the diagram below, a diameter of each of the two smaller circles is a radius of the larger circle. If the two smaller circles have a combined area of $1$ square unit, then what is the area of the shaded region, in square units?

[asy] size(4cm); filldraw(scale(2)*unitcircle,gray,black); filldraw(shift(-1,0)*unitcircle,white,black); filldraw(shift(1,0)*unitcircle,white,black); [/asy]

$\textbf{(A) } \frac{1}{4} \qquad \textbf{(B) } \frac{1}{3} \qquad \textbf{(C) } \frac{1}{2} \qquad \textbf{(D) } 1 \qquad \textbf{(E) } \frac{\pi}{2}$

竟然是1986年AJHSME全美初中数学竞赛第23题的如假包换，一模一样：

The large circle has diameter $\text{AC}$ . The two small circles have their centers on $\text{AC}$ and just touch at $\text{O}$ , the center of the large circle. If each small circle has radius $1$ , what is the value of the ratio of the area of the shaded region to the area of one of the small circles?

[asy] pair A=(-2,0), O=origin, C=(2,0); path X=Arc(O,2,0,180), Y=Arc((-1,0),1,180,0), Z=Arc((1,0),1,180,0), M=X..Y..Z..cycle; filldraw(M, black, black); draw(reflect(A,C)*M); draw(A--C, dashed); label(

$\text{(A)}\ \text{between }\frac{1}{2}\text{ and 1} \qquad \text{(B)}\ 1 \qquad \text{(C)}\ \text{between 1 and }\frac{3}{2}$

$\text{(D)}\ \text{between }\frac{3}{2}\text{ and 2} \qquad \text{(E)}\ \text{cannot be determined from the information given}$

不但问题一样，答案也一样。正可谓是，三十年后，又是一条好汉！

如此举一反三，大同小异，简单的重复，万变不离其宗。掌握了这些规律，多做一些练习，全美数学竞赛，还有什么难的！

What is the value of ?

In the diagram below, a diameter of each of the two smaller circles is a radius of the larger circle. If the two smaller circles have a combined area of square unit, then what is the area of the shaded region, in square units?

The large circle has diameter . The two small circles have their centers on and just touch at , the center of the large circle. If each small circle has radius , what is the value of the ratio of the area of the shaded region to the area of one of the small circles?

What is the value of $1+3+5+\cdots+2017+2019-2-4-6-\cdots-2016-2018$ ?

In the diagram below, a diameter of each of the two smaller circles is a radius of the larger circle. If the two smaller circles have a combined area of $1$ square unit, then what is the area of the shaded region, in square units?