• 十二色定理

   

十二色定理 - 起源又叫Heawood定理。是一种有7个洞的曲面上构造两两相连的12个区域的极限。在人类在企图证明四色定理过程中，发现了在曲面上作图，反而更加容易。参见：八色定理，九色定理，十色定理，十一色定理，七色定理。

十二色定理

曲面染色结构定理

• 提出者

• 德国人林格美国杨斯等证明

• 证明时间

• 1974年

• 适用领域

• 交通枢纽-电路枢纽-芯片

• 
  

定义

 播报

十二色定理 - 起源又叫Heawood定理。人类在企图证明四色定理过程中，发现了在曲面上作图，反而更加容易。

证明四色定理过程联想到曲面染色的问题。

公式来源

1974年德国的林格和美国的杨斯证明了：

证明这个公式，数学家用了78年。P是指这个曲面的洞的个数，又叫亏格。当亏格为7时：

方括号表示取整数。

如果p=7,则是

 即7个洞（又叫亏格7.）需要12个区域才能形成两两相连的形式。每一个区域与其他11个区域相连。

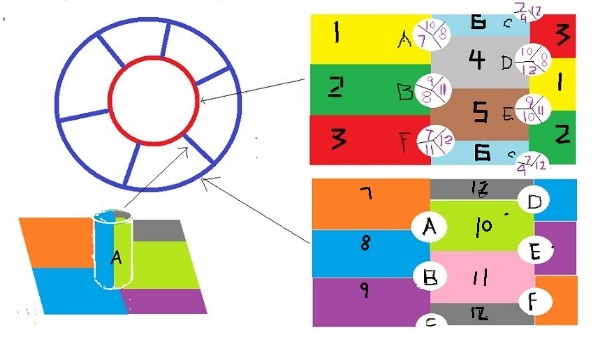
图1，右上面是内环的平面图。右下是外环平面图，大于内环。片面图上下对折再左右对折就是一个轮胎形状。两个轮胎一内一外，外环的ABCDEF有六个延伸的立柱，与内环对应，形成有12个区域两两相连。

公式和公式的证明来自：

《图论导引》214页，机械工业出版社。

王晓明设计并且制造实物体， . 并且给出了这个需要12种颜色染色的图形：

图2，实物图证面

表明：在有7个洞的曲面上染色成为两两相连的区域，11种颜色是不够的。

历史

 播报

数学家在研究四色定理时已经开始考虑曲面染色了，就是说有一百多年历史了，1896年开始推理，1974年完成证明。王晓明设计图形用了3年，制造实物用了2年。

 播报

1974年德国的林格和美国的杨斯证明了上面的公式。

应用

 播报

广泛应用于线路交叉，例如，管道枢纽，电路枢纽（芯片）。可以形成不会堵塞的交通。

影响及意义

论文发表以后，西方工程师已经在考虑应用于芯片设计。 [1] 

• 参考资料