又一个菲尔兹奖桂冠下的数学赝品

2022年国际数学家大会授予詹姆斯-梅纳德菲尔兹奖

，

宣称：2013年，梅纳德用一种新方法证明了张益唐素数定理并大幅改进了其结果，证明了存在无穷多对间隙小于600的素数对，即

。

主项：间隙小于600素数对。

谓项：无穷多个。

      詹姆斯-梅纳德文章错误百出

第1，结论错误

数学证明中的伪证是一种虚假的证明，这种证明不是按照逻辑性规律，而是采用偷换概念或者虚假证据，故意溷淆科学概念与命题的根本差别，企图蒙骗的一种形式。

梅纳德的错误

国际数学界宣称，梅纳德用一种新方法证明了张益唐素数定理并大幅改进了其结果，证明了存在无穷多对间隙小于600的素数对。

梅纳德证明结论使用的是一个集合概念。并且，梅纳德的结论是以特称判断论述的，就不具备基本的可信度，因为所有的数学定理都是全称判断。

梅纳德公式：

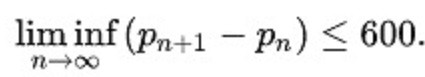
不等式左边表明一种性质，下确界是针对一组数据，极限针对函数和序列，而右边600是说左边的素数对，好了，破绽就在这里。小于600的素数对是一个“集合概念”。集合概念反映的是集合体，集合体有什么不对吗？

    （一）概念的种类：

1，单独概念和普遍概念

a，单独概念反映独一无二的概念，例如，上海，孙中山，，，。它们反映的概念都是独一无二的。数学中的单独概念有“e”“Π”。“e是一个超越数”就是一个主项为单独概念的命题。

b，普遍概念，普遍概念反映的是一个对象以上的概念，反映的是一个“类”，这个词项的内涵由为了包含在词项外延所必须具有的事物的性质组成。例如：工人，无论“石油工人”，“钢铁工人”，还是“中国工人”，“德国工人”，它们必然地具有“工人”的基本属性。数学中的普遍概念有例如“素数”，“合数”，等。

“素数有无穷多个”就是一个主项为普遍概念的命题。

2，集合概念和非集合概念。

a，集合概念反映的是集合体，这个词项的外延由词项所应用的事物集合组成，例如“中国工人阶级”，集合体的每一个个体不是必然具备集合体的基本属性，例如某一个“中国工人”，不是必然具有“中国工人阶级”的基本属性。

b，非集合概念（省略）。

大家明白了吗？梅纳德如果要说间隙不超过600的素数对具有无穷性质，必须对所有小于600的素数对逐一证明，就是要使用完全归纳法：

1）相差2的素数对（这是一个类）无穷。

2）相差4的素数对（类）无穷。

3）相差6的素数对（类）无穷。

.......

300）相差600的素数对（类）无穷。

梅纳德没有确定相差不超过600的素数对都是无穷的。梅纳德等于什么也没有说。顺便说一句，集合概念只是总结归纳，是不需要证明的。

（二），什么是判断？判断就是对思维对象有所断定的形式。

判断的基本性质：

1，有所肯定或者有所否定。

2，判断有真假。

梅纳德没有确定任何一个类是无穷或者有限，梅纳德什么也没有说。就是说，梅纳德的证明违背了一个判断的基本要求，就连一个明确的判断都没有。

数学证明就是要求对数学对象给予一个明确的判断。

（叁）

就算梅纳德想说：“相差不超过600的素数对至少有一对是无穷的”。这个也没有做到一个定理的要求啊？梅纳德是说“有些A是B”,这是一种“特称判断”这样的说法不能作为数学定理，因为数学定理要求明确的“全称判断”，就是“一切A是B”。特称判断在日常生活中使用没有问题，甚至在其它学科也没有问题，例如物理学。唯独在数学证明中特称判断无效。

（四）一个定理陈述一个给定类的所有数学元素不变的关系，适用于无限大的类，在任何时候都无区别成立。梅纳德公式左边的变量部分输入一个值，得出结果是需要区别的，就不是定理了，这些结果，人们无法知道，梅纳德自己也无法知道：“无穷还是有限”。或者说右边600以内的任何一个值对应左边是什么？是无法知道的。

（五）特称判断为什么不能作为定理？

因为特称判断暗含“假定存在”的非逻辑前提，数学证明是严禁使用非逻辑前提，在逻辑学也不允许引入非逻辑前提。这是我们数学中常常发现一个显然的事实却不能成为定理的困难。如果可以引入非逻辑前提，那么数学难题就不会有这么多了。

（六）数学公式是数量关系的固定模式，

梅纳德公式具备一个错误公式的全部特征：

错误公式特征：

1，自称是科学的，但含煳不清，缺乏具体的度量衡。

2，无法使用操作定义(例如，外人也可以检验的通用变量、属于、或对象)

3，无法满足简约原则，即当众多变量出现时，无法从最简约的方式求得答桉。

4，使用暧昧模煳的语言，大量使用技术术语来使得文章看起来像是科学的。

5，缺乏边界条件：严谨的科学公式在限定范围上定义清晰，明确指出预测现象在何时何地适用，何时何地不适用。

梅纳德自己也不知道n值输入后是什么情况。

                                第二，陈述错误

你完成一个数学命题的证明，你应该怎么样陈述才能清晰无误呢？有什么规定吗？数学定理的陈述必须严格按照语法

（一），怎样陈述

对科学（数学）结论陈述，有着明确的要求，就是应该严格按照语法要求，清晰地无歧义地陈述。按照汉语习惯，主项在前，谓项在后。主项和谓项不得分拆成为几个部分。

例如：

“素数有无穷多个”（A具有性质B，素数是主项，无穷多个是谓项，一切A是B，全称判断主项A周延，肯定判断谓项B不周延）

（二）

看看梅纳德怎么样陈述：“存在无穷多个素数对，间隙小于600”。

主项是：间隙小于600素数对。

    谓项是：无穷多。

按照语法规则，主项“间隙小于600素数对”周延，就是全部断定了“无穷多”。但是，作者没有证明这个命题，不敢说那一对是无穷的，只能颠倒次序，把主项非法（语法）分拆两个部分，一部分（素数对）放在前面，一部分是修饰和限定主语的定语（小于600）放在后面。并且把谓项放在前面，，，这个就叫做语无伦次。是违法语法规则的。

表明作者思维矛盾无法通过正确的语言表达。语言的清晰表明思想的清晰，思想的清晰必然要通过清晰的语言完成。