《走近混沌》-25-27-全文完

第二十五章﹕生命游戏-1

 

前面我们介绍了自组织现象和孤子现象。此类现象出现的原因，都与外力无关，而只与系统自身内部各单元之间的相互作用，特别是非线性作用有关。由于这种内部作用，通过自身演化，使得系统群体表现出某种自动结合在一起、形成有序结构的集体行为。

除了物理学之外，科学界的各个领域，以及社会、人文、经济、网络、市场等方方面面，都观察到无序到有序的转化过程。其中，生命进化是大家熟知的例子。生命起源一直是个重大的不解之谜，至今仍然众说纷纭。生命之谜藏身于DNA分子的自我复制现象中，DNA的自我复制需要蛋白质的参与，而蛋白质产生又依赖于DNA携带的信息，这话听起来有点像通常人们开玩笑时所调侃的“先有蛋还是先有鸡”的悖论。事实上也是如此，这个鸡与蛋的基本问题可以说至今未解，因为它在本质上问的就是生命如何起源？

无论如何，生命起源与自我复制的机制有关，科学家们很早就认识到这点。生物学家们在实验室里研究分子如何自我复制的问题，而数学家及理论物理学家们则希望用某种数学模型，在计算机上来模拟产生自我复制的现象。早在上世纪50年代，大数学家冯·诺依曼为模拟生物细胞的自我复制而提出了‘自动细胞机’的概念。但当时并未受到学术界重视，直到1970年，随着计算机技术的普及，剑桥大学的约翰·何顿·康维设计了一个叫做《生命游戏》的电脑游戏之后，‘自动细胞机’这个课题才吸引了科学家们的注意。

一九七零年十月, 美国趣味数学大师马丁·加德纳通过《科学美国人》杂志的“数学游戏”专栏, 将康维的“生命”游戏介绍给学术界之外的广大读者，一时吸引了各行业一大批人的兴趣。

所谓生命游戏，事实上并不是通常意义上的”游戏”, 它没有游戏玩家各方之间的竞争, 也谈不上输赢，可以把它归类为“仿真游戏”。事实上，也是因为它模拟和显示的图象，看起来颇似生命的出生和繁衍过程而得名为“生命”。

 

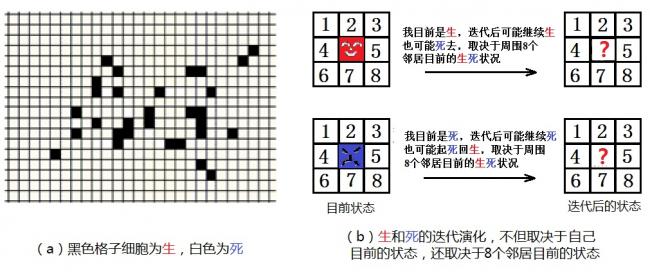
图（25.1）：生命游戏是二维的‘自动细胞机’

游戏在一个类似于围棋棋盘一样的，但格子更为密集、数目更多、可以无限延伸的二维网中进行。例如，设想如图（25.1a）的方格网。每个方格中都可放置一个生命细胞，每个生命细胞只有两种状态：“生”或“死”。在图（25.1a）的方格网中，我们用黑色的方格表示该细胞为“生”, 空格（白色）表示该细胞为“死” 。或者换句话说，方格网中的黑色部分表示的是某个时候某种‘生命’的分布图。生命游戏想要模拟的就是：随着时间的流逝，这个分布图将如何一代一代的变化？

这里又要用上我们在本系列文章中已经打过多次交道的‘迭代法’。在此我们不妨回忆一下曾经用过的迭代法：我们用迭代法画出了曼德勃罗集、朱利亚集等各种分形；用迭代法研究过逻辑斯蒂系统中的倍周期分岔现象，系统的稳定性、从有序到无序的过渡；还用迭代法求解洛伦茨方程及限制性三体问题的数值解。那么，这生命游戏用的迭代法有点什么不同呢？在画分形图和倍周期分岔图时，我们考虑的是系统的‘长期行为’，画出的是固定的，不随时间而变化的图形；画微分方程的数值解时，曲线是随时间而变化的函数，但是那只是空间中的一个点的轨迹。而在生命游戏中，考虑的是整个平面上的‘生命细胞’分布情况的演化过程。也就是说，平面上每个点的‘生死’状态都在不停地变化着。可想而知，这种迭代过程看起来将会生动有趣多了，否则，怎么会把它称之为‘游戏’呢。

游戏开始时, 每个细胞可以随机地（或给定地）被设定为“生”或“死”之一的某个状态, 然后，根据某种规则，计算出下一代每个细胞的状态，画出下一代的生死分布图。

应该规定什么样的迭代规则呢？我们需要一个简单的，但又反映生命之间（格子和格子之间）既协同、又竞争的生存定律。为简单起见，最基本的考虑是假设每一个细胞都遵循完全一样的生存定律；再进一步，我们把细胞之间的相互影响只限制在最靠近该细胞的8个邻居中，参考图（25.1b）。也就是说，每个细胞迭代后的状态由该细胞及周围八个细胞目前的状态所决定。作了这些限制后，仍然还有很多方法，来规定‘生存定律’的具体细节。

例如，在‘康维的生命游戏’中，规定了如下三条‘生存定律’，（被称为规则B3/S23）：

1．   如果8个邻居细胞中，有3个细胞为生，则迭代后该细胞状态为生；

2.       如果8个邻居细胞中，有2个细胞为生，则迭代后该细胞的生死状态保持不变；

3.       在其它情况下，迭代后该细胞状态为死。

上面的三条生存定律，你当然可以任意改动，发明出不同的‘生命游戏’。但那几条规则，也不是游戏的发明者康维随便想当然定出来的，其中暗藏着周围环境对生存的影响在内。比如第一条，8个邻居中有3个是活的，不多不少，这种情况也许对中间的小生命是最理想的，因此，迭代后结果总是为‘生’；第二条，8个邻居中有2个是活的，人气不太旺盛哦，不过也还算马马虎虎吧，对中间的小生命影响不大，所以康维认为，生死可以维持原状；第三条就包括了好几种情况啦，一是8个邻居中活的数目多于4个，太挤啦，将造成物质缺乏，只有死路一条；或者是，8个邻居几乎全死光了，顶多只有一个奄奄一息的，那样的话，中间的小生命也难以生存，死定了。

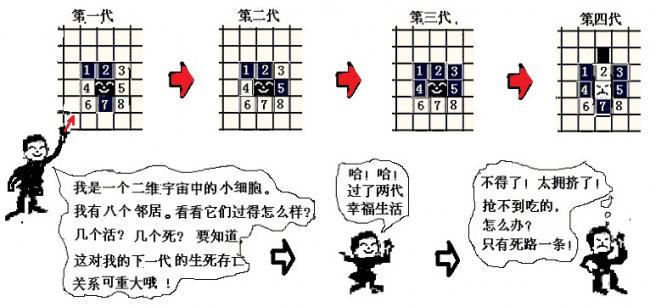
如此定下了生存定律之后，对格子网的某种初始分布图，就可以决定每个格子下一代的状态，然后，同时更新所有的状态，得到第二代的分布图。这样一代一代地作下去，以至无穷。比如说，在图（25.2）中，从第一代开始，画出了四代细胞分布的变化情况。第一代时，图中有四个活细胞（黑色格子），然后，读者可以根据以上所述的四条生存定律，得到第二、三、四代的情况，观察并验证图（25.2）的结论。

 

  图（25.2）：二维生命细胞的四代演化过程

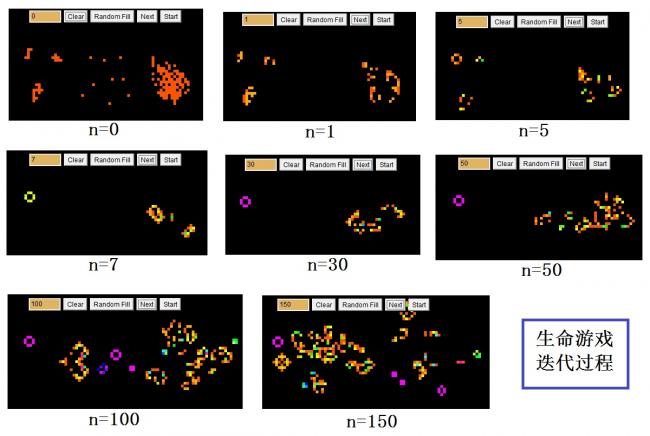
你可能会说，这样的游戏玩起来真是太不方便了！一格一格地算半天才走一步，也看不出趣味在何处。不过，有了计算机的帮助，就不难发现生命游戏的趣味所在了。我们可以根据四条生存定律编好程序，输入初始状态图，用计算机很快地来进行一代一代的运算和显示。图（25.3）所演示的便是计算机的仿真结果，初始分布如图中n=0的小图所示，接下来，便是第5、7、30、50、100、150代之后的分布图。需要注意，图中计算机画出的图形颜色正好与我们刚才的规定相反：黑色背景部分表示没有‘生命’，其余的彩色部分（除黑色之外的任何颜色）则表示生命的分布情形。

 

图（25.3）：计算机模拟的生命游戏迭代过程

（这个计算机生成的图中，黑色部分表示‘死’，其它彩色表示‘生’）

点击图像连接到生命游戏程序

http://www.tianfangyetan.net/cd/java/Life.html

如果仔细观察图（25.3）所示生命游戏图形的演化过程，能发现几个有趣现象。看看最初始的分布图（n=0）中，可将‘活’的细胞分为左中右三群：左边一群不密不疏，最后的演化结果只剩下了一个固定的四边图形；中间的那一群非常分散，人烟过分稀少，第二代就全部死光了；最为有趣的是右边那一群，开始时人口密集，挤得够呛！因此第二代也死掉不少。但是后来，人口逐渐迁移分散，群体得到了更大的空间，从n=50之后，这群人口大幅度增长，子孙繁衍到各处。

第二十六章﹕生命游戏-2

林童在计算机上，玩自己刚写出的‘康维的生命游戏’程序。看着屏幕上五彩缤纷的图像，跳跃不止的点点色彩，像夜空中闪烁不停的星星一样，林童心中泛起一股成就感。特别当他设置出各种初始分布情形，玩了一阵之后，林童更加感到兴趣盎然。

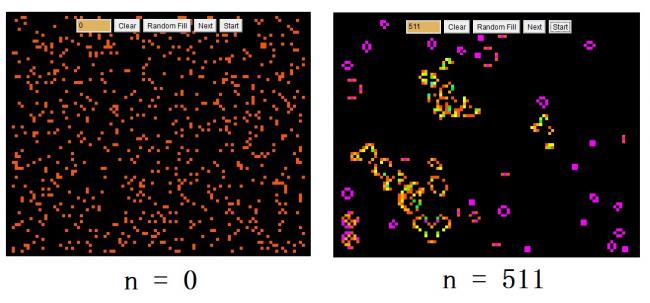
例如，如果你选择“随机设置”作为游戏的初始分布，你会看到，游戏开始运行后的迭代过程中，细胞生生死死，增增减减，变幻无穷。屏幕上“生命细胞”的图案运动变化的情况，的确使人联想到自然界中某种生态系统的变化规律：如果一个生命，其周围的同类过于稀疏，生命太少的话，会由于相互隔绝，失去支持，得不到帮助而死亡；如果其周围的同类太多而过于拥挤时，则也会因为缺少生存空间，且得不到足够的资源而死亡。只有处于合适环境的细胞才会非常活跃，能够延续后代，并进行传播。林童也注意到，游戏开始时的混乱无序的生命随机分布，在按照康维的生存规律，迭代了几百次之后，总是形成一些比较规则的图案，像图（26.1）所示的那样。这看起来确实有点类似‘无序到有序’的转化，或者是，李四说的‘自组织现象’。游戏的演化方向和热力学第二定律描述的那种‘趋于平衡’的演化方向大相庭径，这个游戏真能和‘生命起源’、或‘生命进化’，沾上点儿边吗？

图（26.1）：生命游戏模拟‘无序到有序’

生命游戏激起了林童对生命科学的兴趣，脑海里模糊地确定了一个自己将来发展的方向：用计算机技术来研究生命科学。不过当前，他饶有兴味地看着图（26.1）中n=511的那张图，其中的图案使他浮想联翩。计算机屏幕上，随着n的增大，图案不断变化：有的图案最后定居在某个位置，似乎永远不变了，除非远方来的侵略者突然出现在旁边，这种固定类型图案使林童想起收敛于一点的经典吸引子；有的群体，则作很规则的振动，在几个图案之间不停地循环跳跃，就像逻辑斯蒂系统分岔成双态平衡和多态平衡时的情形那样；还有几种图案，颇似太空船、游艇、或汽车，逍遥自在地周游四方；有的群体，在不断游走的同时，自身图案的形状也变换无穷，这种情形是不是和逻辑斯蒂系统中出现混沌有点类似呢？从数学上，林童想不出这生命游戏能和逻辑斯蒂混沌系统有什么关系，书上也没见有诸如此类的说法，只不过是似曾相识的现象此处彼处到处可见而已啊！尽管如此，林童仍然觉得这“生命游戏”特别有意思，继续观察研究各种图案。

图（26.1）中n=511的图，的确比n=0的初始图，更有次序多了。其中看上去有序的每种图案又互不相同、各有特色。在图（26.2）中，我们画出了几种典型的分布情形，大概可以把这些图案的演化方式分成下列几种类型：静止型、振动型、运动型、死亡型、不定型。

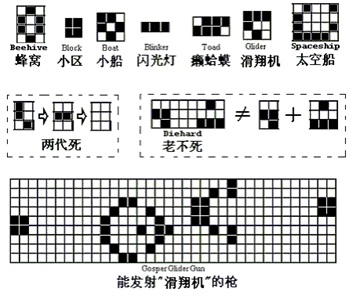
图（26.2）：生命游戏中几种特别类型的分布图案

例如，图（26.2）中的“蜂窝”，“小区” 和“小船”，都属于静止型的图案，如果没有外界的干扰的话，此类图案一旦出现后，便固定不再变化；而“闪光灯”，“癞蛤蟆”等，是由几种图形在原地反复循环地出现而形成的振动型；图中右上角的“滑翔机”和“太空船”，则可归于运动类，它们会一边变换图形，一边又移动向前。如果你自己用生命游戏的程序随意地试验其它一些简单图案的话，你就会发现：某些图案经过若干代的演化之后，会成为静止、振动、运动中的一种，或者是它们的混合物。

此外，也还有可能得到我们尚未提及的另外两种结果：一类是最终会走向死亡，完全消失的图案；另一类是永远不定变化的情形。就拿“最终死亡”的情况来说吧，“死”的速度可是有快有慢，有的昙花一现，不过几代就断子绝孙了（图中的两代死）；有的倒能繁荣昌盛几百上千代：如上图中间的第二个例子就能坚持130代。有趣的是，图中的“老不死”是由两个分图案构成的，这两个分图案如果单独存在，都会长生不死，纠集在一块儿后，尽管也延续了130代，结果却不一样，最后以‘死’而告终。这可看着是一个“整体不等于部分之和”的实例。从变幻莫测的生命游戏中，还有许许多多诸如此类的趣事，我们就不一一列举了。

尽管生命游戏中每一个小细胞所遵循的生存规律都是一样的，但由它们所构成的不同形状的图案的演化行为却各不相同。我们又一次地悟出这个道理：“复杂的事物（即使生命！），原来也可以来自于几条简单的规律！”。生命游戏继分形和混沌之后，又为我们提供了一个观察从简单到复杂的好方式。

生命游戏的发明人约翰·康维，现为美国普林斯顿大学数学教授。康维除了致力于群论、数论、纽结理论及编码理论这些多方纯数学领域之外，也是游戏的热心研究者和发明者。在众多贡献之中，他的两个最重要的成果都与游戏有关：一是他在分析研究围棋棋谱时发现了超实数（Surreal Number）；其二便是他在英国剑桥大学时发明的生命游戏使他名声大振，特别是经由《科学美国人》连续两期的介绍推广后，康维的名字在７０年代的大学及知识界几乎人人皆知。上世纪的７０年代初，使用计算机还只是少数科研人员的专利，对生命游戏中图案演化行为的研究，有些热心者甚至利用业余时间在纸上进行！据马丁·加德纳后来回忆所述，当时整个国家科研基金的用途中，可能有价值上百万美元的计算机时间，花费于并不十分合法的对“生命”游戏的探索。业余爱好者疯魔于此游戏的规则简单却变化无穷; 生物学家从中看到了”生态平衡”的仿真过程; 物理学家联想到某种似曾相识的统计模型; 而计算机科学家们则竞相研究“生命游戏”程序的特点, 最后，终于证明了此游戏与图灵机等价的结论。对生命游戏过分的热心和疯狂，大大超出了《科学美国人》的“数学游戏”专栏的负荷能力，以至于当时还专门为此推出了一个名为《生命线》的通讯刊物。

另一件值得一提的趣事是：康维当时设置了一个五十美元的小奖金，给第一个能证明生命游戏中某种图形能无限制增长的人。这个问题很快就被麻省理工学院的计算机迷Bill Gosper解决了，这就是图（26.2）中最下面一个图案“滑翔机枪”的来源。图（26.3）所示的是滑翔机枪在计算机上运行的情形：一个一个的“滑翔机”永不停止地、绵绵不断地被“枪”发射出来。

 

图（26.3）：生命游戏中的滑翔机枪

这个实例证明了生命游戏中存在无限增长的情形，看起来的确令人鼓舞：由几条简单的“生存定律”构成的“宇宙”中的“枪”，能不断地产生出某种东西，就象机器制造出产品一样。那么，是否可能再进一步，找到某种图案在演化过程中能自我复制，象生命形成的过程一样呢？这不也正是冯·诺依曼当时提出‘自动细胞机’的原始想法吗？

康维的生命游戏的规则是可以改动的。于是，便产生了将生存定律稍加改动的‘生命游戏系列’，1994年，一个叫Nathan Thompson的人发明了HighLife游戏，将生存定律从康维的B3/S23改为B36/S23，并且从这个游戏得到自我复制的图案^【1】。再后来，也有人从原版的康维生命游戏得到自我复制现象。

 

林童激动地告诉刚走进房间的王二和林零，用生命游戏可以观察到自我复制的图案，解决生命起源之谜已经为时不远啦，却不料被王二嘲笑了一番：

 

“别太幼稚啦，那不过是个游戏，离真正的、生物学意义上的生命还相距十万八千里呢！计算机当然是个仿真大自然的好工具，但毕竟只是仿真，不是真的。不要像那个什么史蒂芬·沃尔弗拉姆似的，以为计算就能解决一切问题了，真是大惊小怪、异想天开！”

 

林童被王二嘲笑得十分沮丧，也不知王二所说的沃尔弗拉姆，是何方神圣？不过读者别为他着急，且读下文，方知分晓。

 

参考资料：

 

【1】http://en.wikipedia.org/wiki/HighLife

【2】生命游戏Java：http://www.bitstorm.org/gameoflife/

第二十七章﹕初级细胞自动机

 

西方有句谚语：“在木匠眼里，月亮也是木头做的。”

古希腊哲学家泰勒斯说：万物之本是水。他的学生毕达哥拉斯说：万物之本是数。再后来又有赫拉克利特说：万物之本是火。中国哲学家孟子以心为万物之本。近代的哲学家有了物理知识，则说：万物之本是原子、电子等基本粒子。看来，哲学家们和木匠异曲同工，都希望把复杂的世界追根朔源到某一种简单的、自己理解了的东西。

如今这个计算机时代，有人宣称说：万物之本是计算。

这个人就是上世纪80年代后期开发著名的《数学》Mathematica符号运算软件的美国计算机科学家，史蒂芬·沃尔弗拉姆(Stephen Wolfram)。

实际上，沃尔弗拉姆并不是提出“万物之本是计算”的第一人。MIT计算机实验室前主任弗雷德金，早在上世纪80年代初就提出：“终极的实在不是粒子或力，而是根据计算规则变化的数据比特。”著名物理学家费曼在1981的一篇论文里也表达过类似的观点。

不过，沃尔夫勒姆沿着这条路走得更远。从古至今困扰人们的三个基本哲学问题：生命是什么？意识是什么？宇宙如何运转？按照沃尔夫勒姆在他的砖头级巨著“新科学”里的“计算等价原理”，生命、意识都从计算产生，宇宙就是一台‘细胞自动机’。

被人们称为天才的沃尔弗拉姆一九五九年生于伦敦，十五岁发表他的第一篇科学论文，二十岁获得美国加州理工学院的物理博士学位。之后，又荣获麦克阿瑟基金会的“天才”奖。当时，他将此奖项所获得的十二万五千美元的奖金全部用于了他感兴趣的基本粒子物理及宇宙学等方面的研究。

八十年代初期，即将离开加州理工学院，前往普林斯顿高等研究院进行研究的沃尔弗拉姆在一次研讨会上，初识了“细胞自动机”的理论，颇有一见钟情、相见恨晚的样子，一头扎进细胞自动机的研究之中。

沃尔弗拉姆在八十年代后期，因为开发了著名的《数学》符号运算软件而声名大振，且获得了商业上的成功。进入九十年代后，他便躲进小楼成一统，继续他所痴迷的细胞自动机工作，潜心著作一部“曠世之作”。直到2002年，沃尔弗拉姆奋战10年，经过无数次的敲键盘、移鼠标，终于产生出作者狂妄地自我宣称是“与牛顿发现的万有引力相媲美的科学金字塔”的巨著，名为：《一种新科学》。

在这部1200页的重量级著作中，沃尔弗拉姆将他所偏爱的一维自动细胞机中的“规则 110”的精神光大发扬，贯穿始终。根据书中的观点，各种各样的复杂自然现象，从弹子球、纸牌游戏到湍流现象；从树叶、贝壳、等生物图案的形成，到股票的涨落，实际上都受某种运算法则的支配，都可等价于“规则 110” 的细胞自动机。沃尔弗拉姆认为“如果让计算机反复地计算极其简单的运算法则，那么就可以使之发展成为异常复杂的模型，并可以解释自然界中的所有现象”，沃尔弗拉姆甚至更进一步地认为宇宙就是一个庞大的细胞自动机，而“支配宇宙的原理无非就是区区几行程序代码”。

《一种新科学》的出版在当时引起轰动，初版五万册在一星期之内销售一空，但是，学术界大多数专家们对此书的评价却不高。对沃尔弗拉姆傲慢自大、忽视前人的工作、自比牛顿的做法，更是嗤之以鼻，认为这是使用商业手段，对不熟悉细胞自动机的广大读者的一种误导。事实上，沃尔弗拉姆并未创立什么“新科学”，由冯·诺依曼提出的细胞自动机的理论，已有五十多年的历史，这个理论，以及基于复杂源于简单的道理的‘复杂性科学’，一直都是科学界的研究课题。

沃尔弗拉姆虽然言过其实，但他对细胞自动机的钟爱，对科学的执着，仍然令人佩服。况且，沃尔弗拉姆也不仅仅是空口说白话，而是用计算机进行了大量的论证和研究。比如，他认定了宇宙是个庞大的细胞自动机，但是有很多种不同的细胞自动机啊，宇宙到底是根据哪种细胞自动机运转的呢？我们在上一章中介绍过的康维的生命游戏，只是众多二维细胞自动机中的一种，如果变换生存定律，可以创造出一大堆不同的生命游戏来。此外，除了二维的细胞自动机，还可以有一维、三维、甚至更多维的细胞自动机。那么，宇宙遵循的是哪一种呢？

沃尔弗拉姆想，首先应该从最简单的一维细胞自动机开始研究。

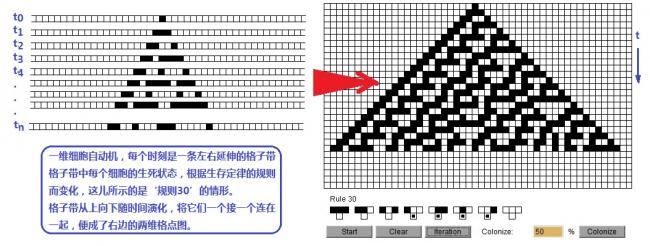
像生命游戏那种二维细胞自动机，是将平面分成一个一个的格子。因此，一维细胞自动机就应该是将一维直线分成一截一截的线段。不过，为了表示得更为直观一些，我们用一条无限长的格点带来表示某个时刻的一维细胞空间，如图（27.1a）所示。用格子的白色或黑色来表示每个细胞的生死两种状态。并且，只考虑最相邻的两个细胞，也就是与其相接的“左”、“右”两个邻居的影响。如此所构成的最简单的细胞自动机被称为初级细胞自动机。

 

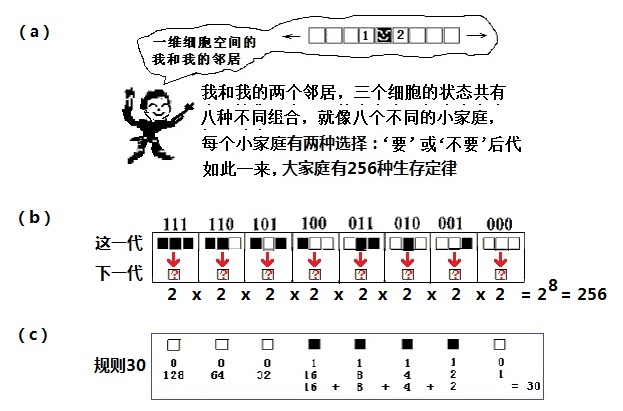
图（27.1）：初级细胞自动机有256种

到底有多少种初级细胞自动机呢？一个细胞加上它的左右两个邻居，这三个细胞的生死状态（输入），决定了该细胞下一代（输出）的状态。因为三个细胞的状态共有八种不同的组合，因此，如图（27.1b）所描述的，初级细胞自动机的输入有八种可能性。对每一种可能的输入，下一代的中间那个细胞都有‘生’或‘死’两种状态可选择。所以，总共可以组合成2⁸=256种不同的生存定律。也就是说，有256种不同的初级细胞自动机。

和我们介绍生命游戏一样，图（27.1b）中用二进制的0（空格）代表‘死’，1（黑色格子）代表‘生’。首先，将输入可能的八种情况按照111、110、101、100、011、010、001、000的顺序从左至右排列起来，然后，八种输入所规定的输出状态形成一个八位的二进制数。将此二进制数转换成十进制，这个小于256的正整数便可用作初级细胞自动机的编码。例如，图（27.1c）所示的输出状态可以用二进制数00011110表示，将其转换成十进制数之后，得到2⁴+2³+2²+2¹ = 30。我们便把这个生存定律代表的初级细胞自动机，称为‘规则30’。

 

图（27.2）：初级细胞自动机‘规则30’的时间演化图

初始时刻只有中间一个细胞为‘生’

Java program

http://mokslasplius.lt/rizikos-fizika/en/wolframs-elementary-automatons

为了显示一维细胞自动机中，细胞状态不同瞬时的演化情况，我们将每一个相继时刻对应的的格点带附在上一时刻对应的的格点带下面。如图（27.2）所示，在t0时刻的格点带，是一条只有中间一个格点为‘黑’，其余格点均为‘白’的左右延伸的长带子。图中，垂直向下的方向表示时间的流逝。因为加了一个时间轴，所以，虽然是一维细胞自动机，而计算机屏幕显示出来的却是一个二维格点图。图（27.2）显示了规则30的演化，图（27.3）给出了更多其它规则的初级细胞自动机的演化图形。

 

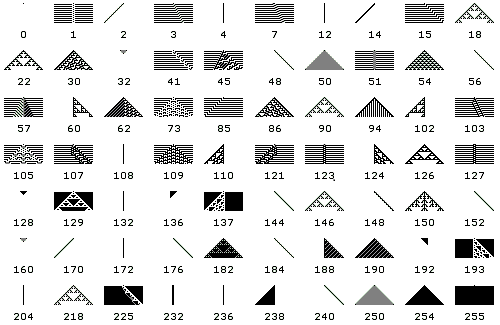
图（27.3）：初级细胞自动机的时间演化图

图像来自Wolfram：

http://mathworld.wolfram.com/ElementaryCellularAutomaton.html

在沃尔弗拉姆发表的一系列论文中，对一维细胞自动机的代数、几何、统计性质作了系统深入的研究和分类。他还特别对其中初级细胞自动机的“规则 30”和“规则 110”的有趣性质情有独钟。图（27.4）给出这两种规则对于随机初始值的时间演化图。“规则 30”之所以特别是因为它的“混沌”行为，例如我们可以考查中心细胞的状态随时间演化所得到的二进制序列：1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, ...，可以证明，这是一个无穷不循环的伪随机序列。“规则 110”则更为有趣：在随机的初始条件下，却产生出好些看起来在一定程度上“有序”、但是又永不重复的图案。“规则 110”似乎揭示了无序中的有序，混沌之中包含着的丰富的内部结构，隐藏着更深层次的规律。沃尔弗拉姆的一个年轻助手库克后来（1994年）证明，“规则 110”是等效于通用图灵机的。

图（27.4）：规则30和规则110

如何理解一个初级细胞自动机“等效于通用图灵机”呢？从生物学的角度看，细胞自动机的每一次迭代变化表现为细胞的生生死死，而从计算机科学的角度，每次演化却可看作是完成了一次‘计算’。

查查计算机的历史，曾经使用过一条长长的穿孔纸带作为输入输出，这听起来和我们这儿每个离散时刻的格子带有些类似。格点带上细胞的黑白生死分布，就对应于计算机纸带上的（0/1）“符号串”。可以想象，如果我们有适当的编码方法，就能将任何数学问题，包括它的初值和算法，变成一列符号串，写到初始的第一条格子带上。然后，根据细胞自动机内定的变换规则，可以得到下一时刻的符号串，也就是说，完成了一次“计算”。依此类推，时间不断地前进，“计算”便一步一步地进行，直到所需要的结果。这个过程，的确与计算机的计算过程类似。

但是，并非所有规则的细胞自动机，都能等同于真正的计算机，还得看看它的智商如何？上面说过，我们有256种不同规则的细胞自动机，它们的智商高低不同，各具有不同的“计算”能力，。

例如，让我们考查一下图（27.3）所显示的256个初级细胞自动机中的几个特例：

1.  首先，象“规则 255”这样的，完全谈不上什么计算能力，连“识别”能力都没有，因为无论对什么“数”，经它“计算”一次之后，全部一抹‘黑’，这点从它的规则定义也可看出来；“规则0”也一样，全部一抹‘白’。

2.  接着，我们再来看象“规则 90”那一类的，时间演化图有点象帕斯卡三角形的那种。这种情况的结果太规矩了，一个呆脑瓜，肯定计算能力有限，第一条的数据再复杂，犹如“对牛弹琴”一样。

3.  另外，象“规则 30”那样的，似乎较好一些，但逻辑杂乱无章，是个胡作非为、不听指挥的家伙。

4.  最后，唯有像“规则 110”这样的，计算能力才达到标准，被证明与通用图灵机是计算等效的。

…………

林童看完了有关‘初级细胞自动机’的介绍，闭着眼睛遐思冥想。王二没错！月亮的确不是木头做的，我们的世界也不能单靠计算而算出来。但是，分形、混沌、以及非线性科学中的这些数学模型，以及计算机迭代的方法，对理解大自然还是很有用处的。林童想，科学真是太有趣、太迷人了！科学就像一座美丽宏大的花园，从分形和混沌这几支科苑奇葩，他似乎看到了满园的绿草如茵、花果飘香。林童想着想着，不知不觉地进入了梦乡，梦中，他倘佯在百花丛中……

×××××××××××××××××××××××××××××××××××××××××××××＊＊＊＊＊＊＊＊

××　 　如果想继续看我的系列科普的万维网友，请到如下地址：  　　　　　　**

***　　科学网博客：http://blog.sciencenet.cn/u/tianrong1945 

＊＊  　系列科普目录：http://blog.sciencenet.cn/blog-677221-601960.html