又见兔子

定义：

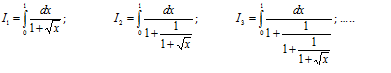
求

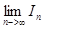
We first introduce Fibonacci numbers.

f(0) = f(1) = 1,

f(n) = f(n-1) + f(n-2), n ≥ 2.

In integral I(n), let x = y*y. It is not hard to prove that the integrand is

2y {[f(n-1) + f(n-2)y]/[f(n) + f(n-1)y]} ≡ 2y g(n, y).

We will omit y inside g(n, y) as g(n).

Fibonacci number f(n) has the asymptotic  form sqrt(5)/x0^n where x0 is the Golden Ratio 0.618… Using this asymptotic  form, after simplification,

g(n) ≈ x0

I(n) ≈ x0 = [sqrt(5) – 1]/2.